adaptive

Adaline: ottimizzazione con la normalizzazione del dataset

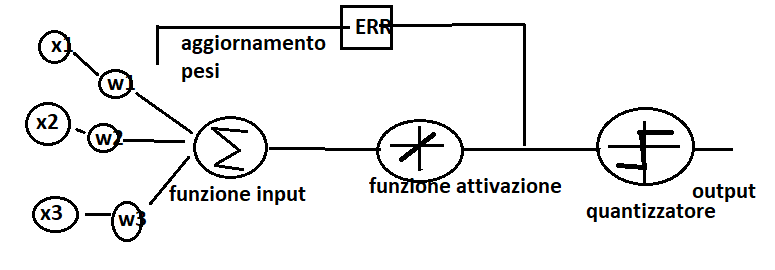
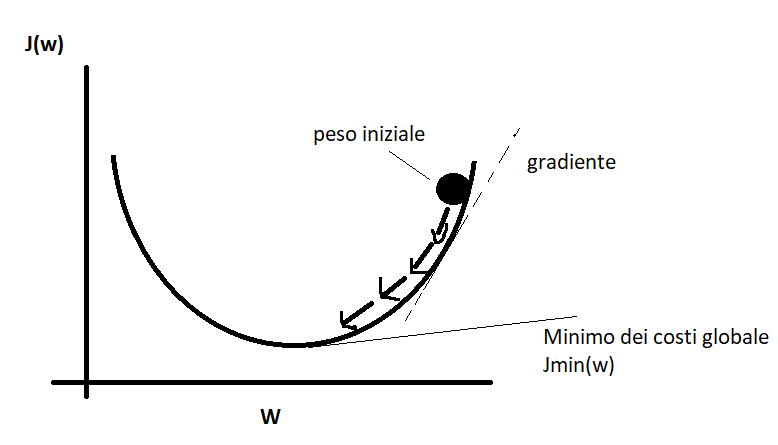
Prendendo spunto dal paragrafo precedente per ottimizzare l’algoritmo di Adaline in modo che la funzione costo venga minimizzata in maniera più veloce allora è possibile standardizzare l’intero dataset con la normalizzazione delle caratteristiche.

In che modo possiamo normalizzare? usando la distribuzione normale standard. la distribuzione normale standard prevede

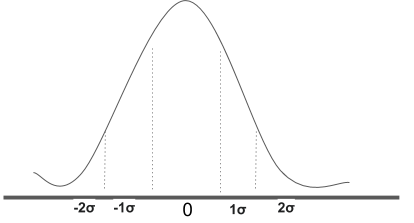
Per normalizzare il dataset basta prendere ogni caratteristica, sottrarla per la media della distribuzione normale μ e dividere tutto per la deviazione standard σ

Ad esempio, per standardizzare la caratteristica j-esima è necessario prima sottrarre la media μ_j poi dividere per σ_j .

x^‘_j = (x_j – μ_j)/σ_j

Addestriamo ora lo stesso algoritmo Adaline utilizzato nel paragrafo precedente con il dataset normalizzato. La libreria numPy ha già funzioni per calcolare la deviazione standard e la media.

Anzitutto vediamo nel grafico i valori normalizzati,

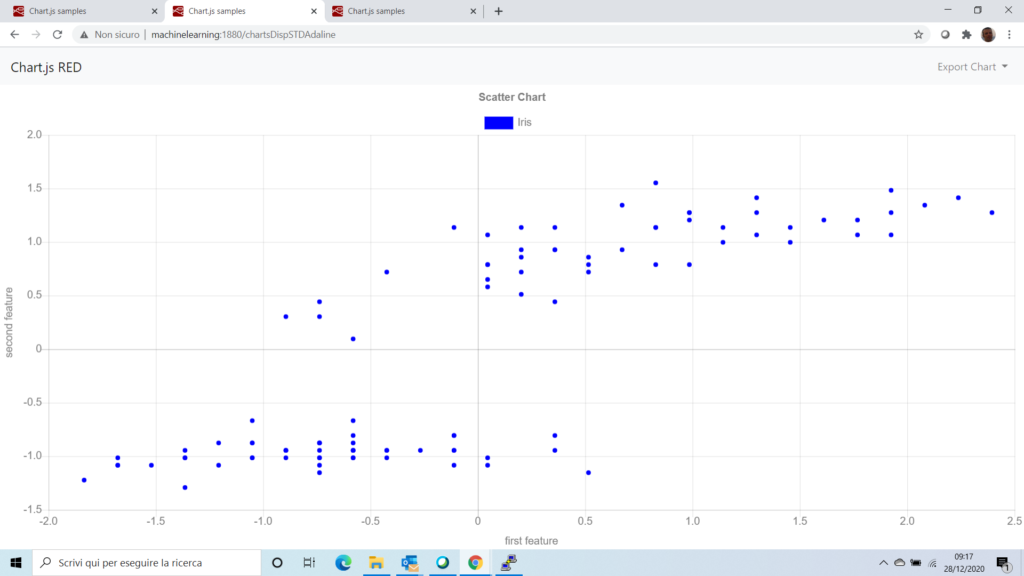
Addestriamo l’algoritmo con questi dati, dopo di che, osserviamo il grafico dei costi

pn = Adaline(0.01, 15)
pn.fit(X_std, y)

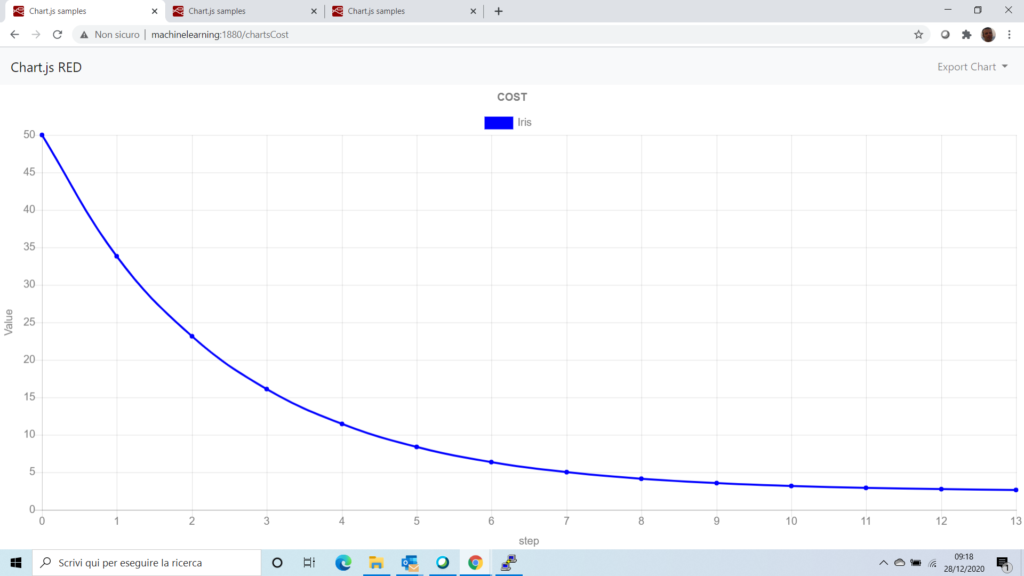
Il grafico mostra chiaramente la convergenza della funzione dei costi a fronte di un dataset normalizzato.

Giusto per fare un confronto mostriamo lo stesso grafico dei costi addestrando l’algoritmo con il dataset non normalizzato.

funzione di costo con dataset non normalizzato

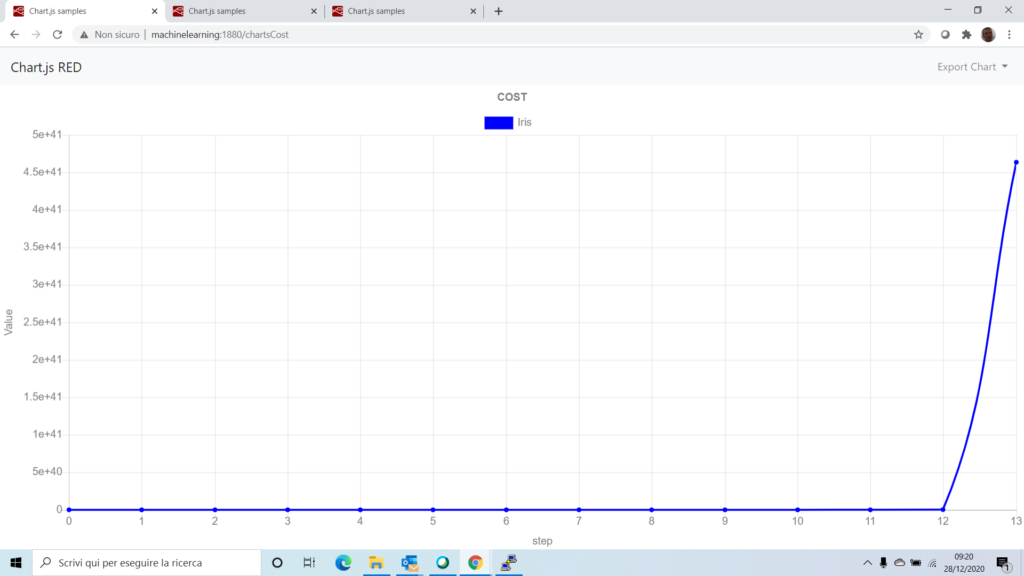
Come volevasi dimostrare, la funzione di costo viene nettamente ottimizzata utilizzando il dataset normalizzato.

Adaline: MachineLearning con supervisione, algoritmo adattivo lineare

L’algoritmo Adaline (ADaptive LInear NEuron) è un algoritmo di convergenza dell’apprendimento. Ciò vuol dire che i pesi non si aggiornano ad ogni epoch sulla base di una funzione di attivazione binaria (come nel caso del Perceptron), ma si aggiornano sulla base di una funzione di attivazione lineare.

Come vediamo nel grafico sopra, la differenza con l’algoritmo Perceptron è che i pesi si aggiornano attraverso una funzione lineare ad ogni epoch. Questo consente di minimizzare la funzione di costo.

La funzione di costo è la funzione J che apprende i pesi in termini di somma dei quadrati degli errori (Sum Squared Errors – SSE) fra il risultato calcolato e la vera etichetta della classe.

J(w) = 1/2 Σ_i (y⁽ⁱ⁾ – Φ (z⁽ⁱ⁾))²

Quali sono i vantaggi di questa funzione? Questa funzione di costo è differenziabile ed è convessa. Questo ci consente di utilizzare un algoritmo di discesa del gradiente per trovare i pesi che minimizzano la funzione di costo.

Come si può vedere nel grafico sopra, i pesi si aggiornano in base alla funzione di costo descritto in precedenza. A partire quindi da un peso iniziale (w), i pesi si aggiorneranno fino a raggiungere il minimo dei costi globale ed allontanandoci quindi dal gradJ(w)

Il cambiamento del peso è definito in questo modo:

Δ(w)= -η gradJ(w)

Per calcolare il gradiente è necessario fare la derivata parziale della funzione J ad ogni peso w_i. Il vantaggio dell’algoritmo è che i pesi vengono aggiornati simultaneamente a differenza del Perceptron che venivano aggiornati ad ogni iterazione.

Post Correlati