Autore: admin

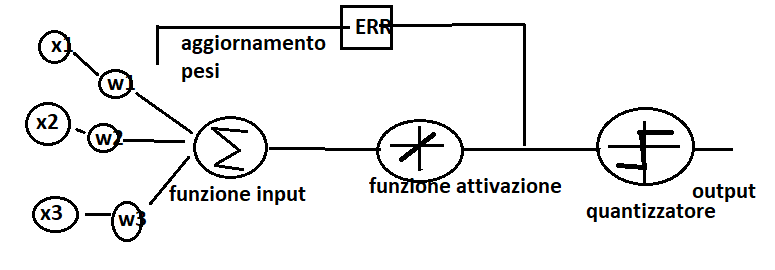
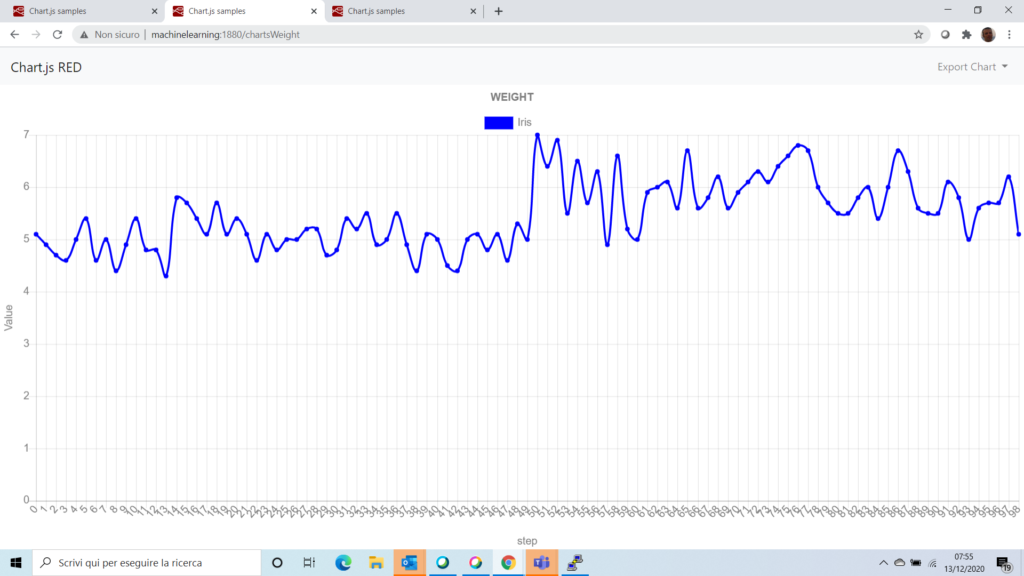
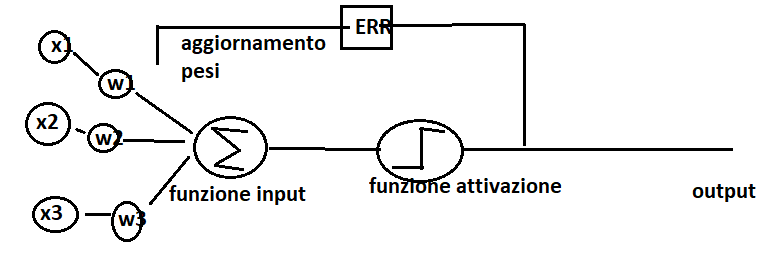
Per analizzare le performance dell’algoritmo Perceptron prendiamo in esame un dataset molto studiato nell’ambito della machine learning: l’insieme delle caratteristiche della lunghezza e larghezza dei petali capaci di riconoscere una particolare famiglia Iris.

Per fare questo ci serviremo di importanti librerie di scikit-learn

anzitutto preleviamo il dataset

# load dataset
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target

definiamo tramite le funzioni di scikit-learn il training-set ed il testing-set e standardiziamo i campioni

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.4, random_state = 1, stratify = y)

sc = StandardScaler()
sc.fit(X_train) # calculate mu and sigma
X_train_std = sc.transform(X_train) # standardize
X_test_std = sc.transform(X_test)

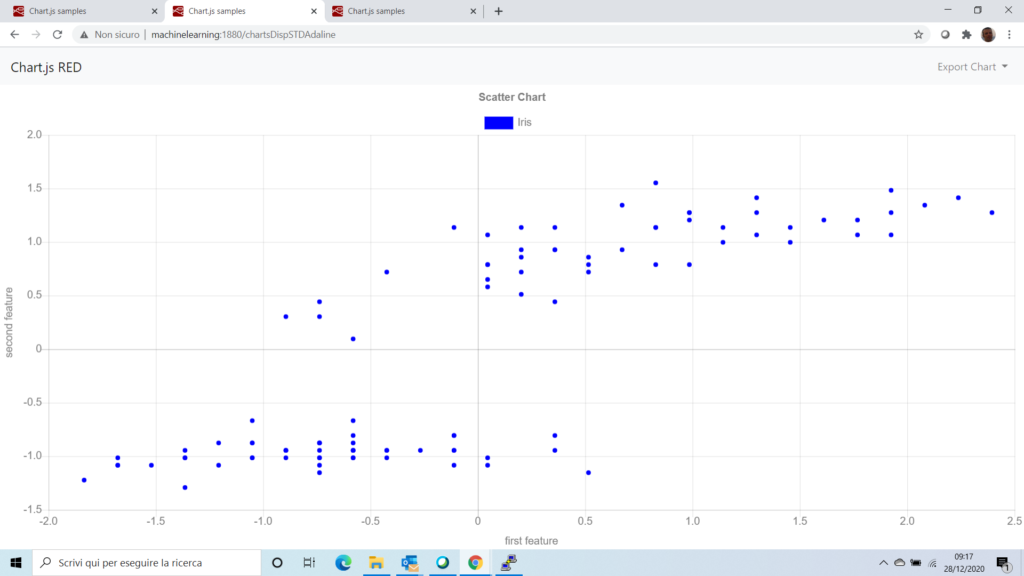
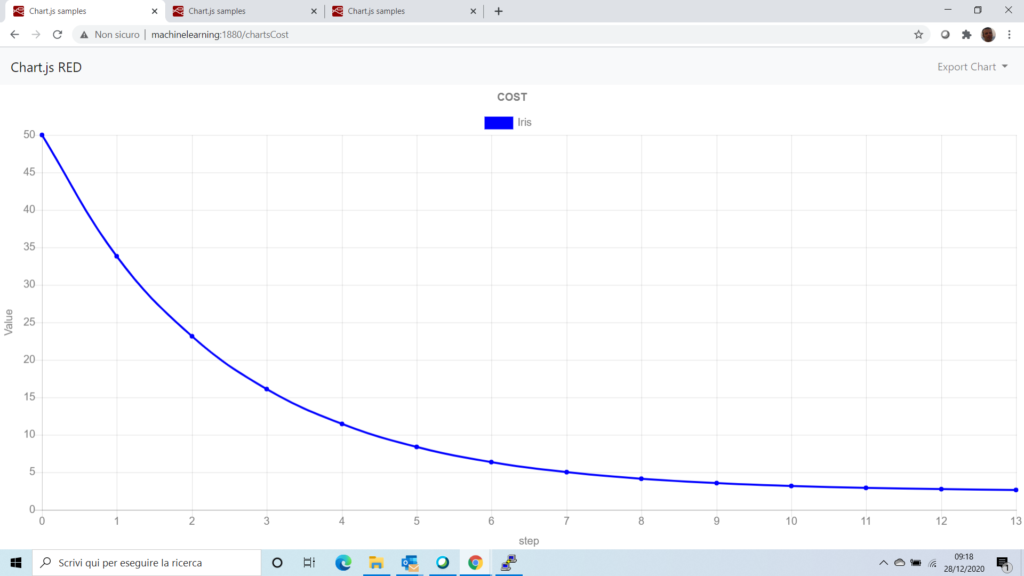
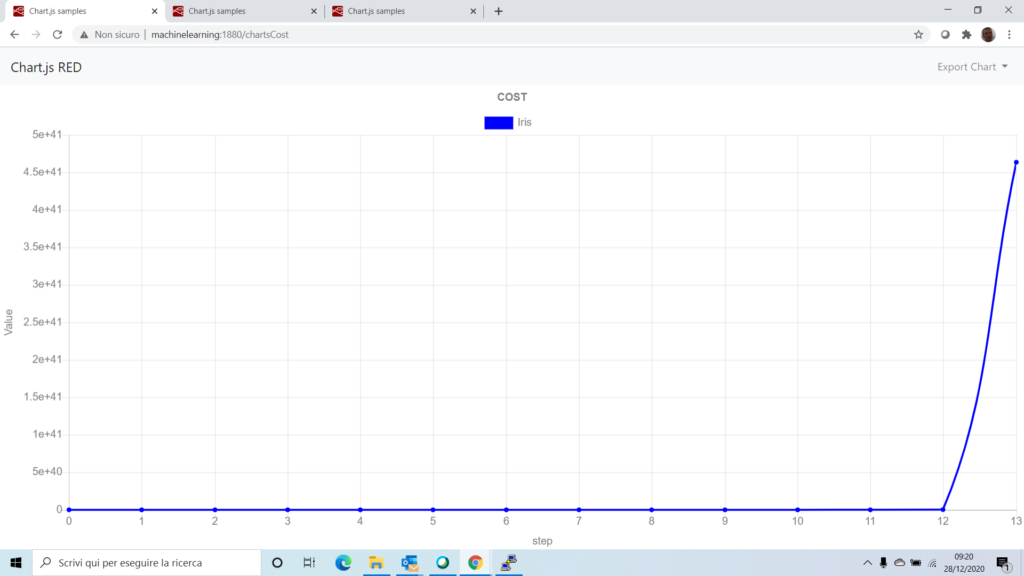
utiliziamo il perceptron per risolvere il problema della classificazione e misuriamone le performance rappresentando i dati su un grafico. Parametriziamo il Perceptron con un numero di epoch pari a 50 ed un tasso di apprendimento pari a 0.2.

ppn = Perceptron(max_iter = 50, eta0 = 0.2, tol = 1e-3, random_state = 1)
ppn.fit(X_train_std, y_train)
y_pred = ppn.predict(X_test_std)
err =(y_test != y_pred).sum()
acc=(y_test == y_pred).sum() / len(y_test)

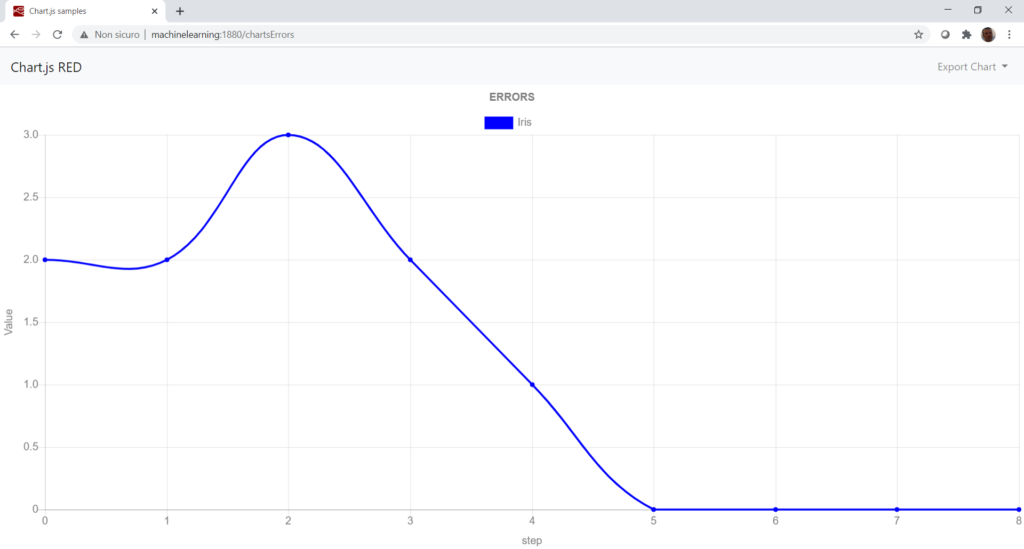
plt.plot(err)
plt.xlabel('wrong classification')
plt.show()

risultato:

y label count : [50 50 50]
y_train label count : [35 35 35]
y_test label count : [15 15 15]
wrong sample : 3
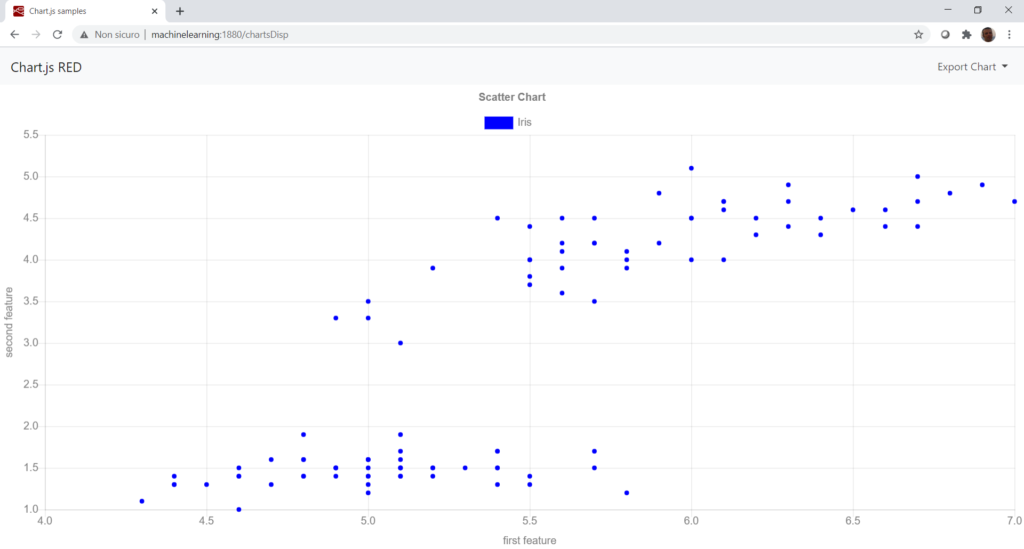
perceptron accurancy : 0.931

rappresentazione grafica dei dati.

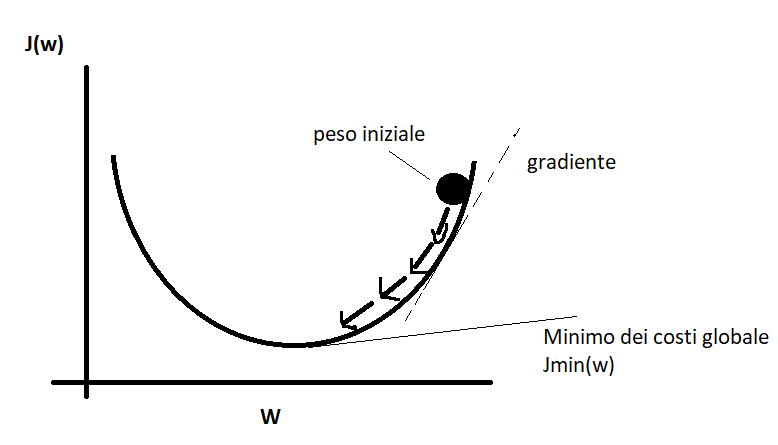
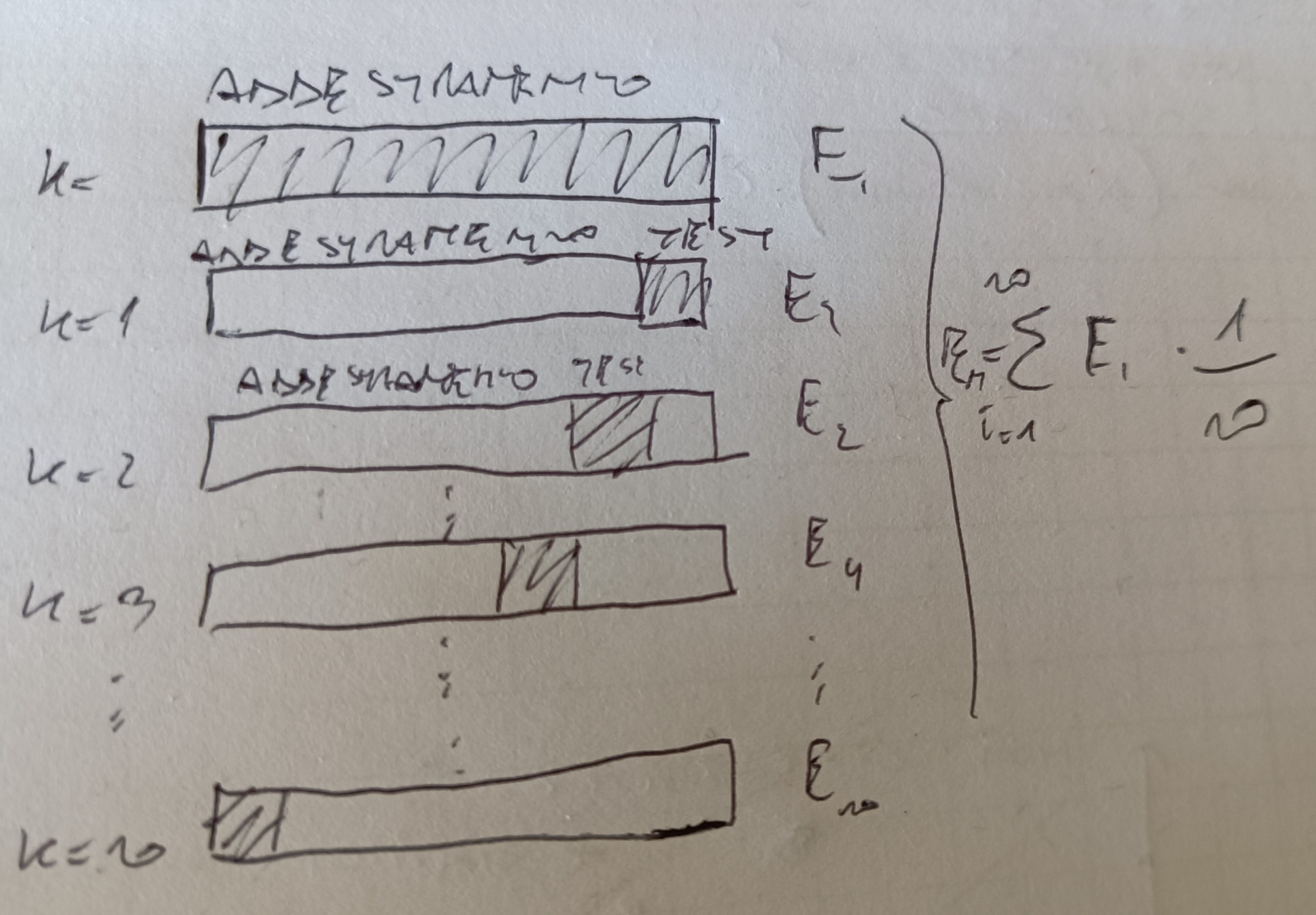
Una tecnica per misurare le performance di un modello è selezionare gli iperparametri di un algoritmo (ovvero i parametri che rendono l’algoritmo più efficiente rispetto la stima che si vuole avere) si chiama K-Fold.

La tecnica consiste nel suddividere il dataset in k parti senza reinserimento. K-1 viene usato per il test di addestramento, la restante parte viene usata per il test.

Per ogni fold viene calcolata la prestazione del modello ed infine viene calcolata la media delle prestazioni per tutti i fold. Vedi figura.

#searching performance

#K-FOLD Stratified
skf = StratifiedKFold(n_splits=2)
skf.get_n_splits(X, y)

print(skf)

scores=[]


for train_index, test_index in skf.split(X, y):
        print("data train:", train_index, "data test:", test_index)
        X_train, X_test = X[train_index], X[test_index]
        y_train, y_test = y[train_index], y[test_index]
        pipe_lr.fit(X_train, y_train)
        score=pipe_lr.score(X_test,y_test)
        scores.append(score)
        print('test accurancy: %.3f ' %score)
print ('total accourancy: %.3f +/- %.3f ' %np.mean(scores), np.std(scores))


#CROSS VALIDATION SCORE
from sklearn.model_selection import cross_val_score
scores = cross_val_score(estimator=pipe_lr, X=X_train, y=y_train, cv=10, n_jobs=1)

print ('total accourancy: %.3f +/- %.3f ' %np.mean(scores), np.std(scores))

Il risultato

Class label : [0 1 2]
y label count : [50 50 50]
y_train label count : [35 35 35]
y_test label count : [15 15 15]
wrong sample : 3
perceptron accurancy : 0.93